ZUM-Unterrichten







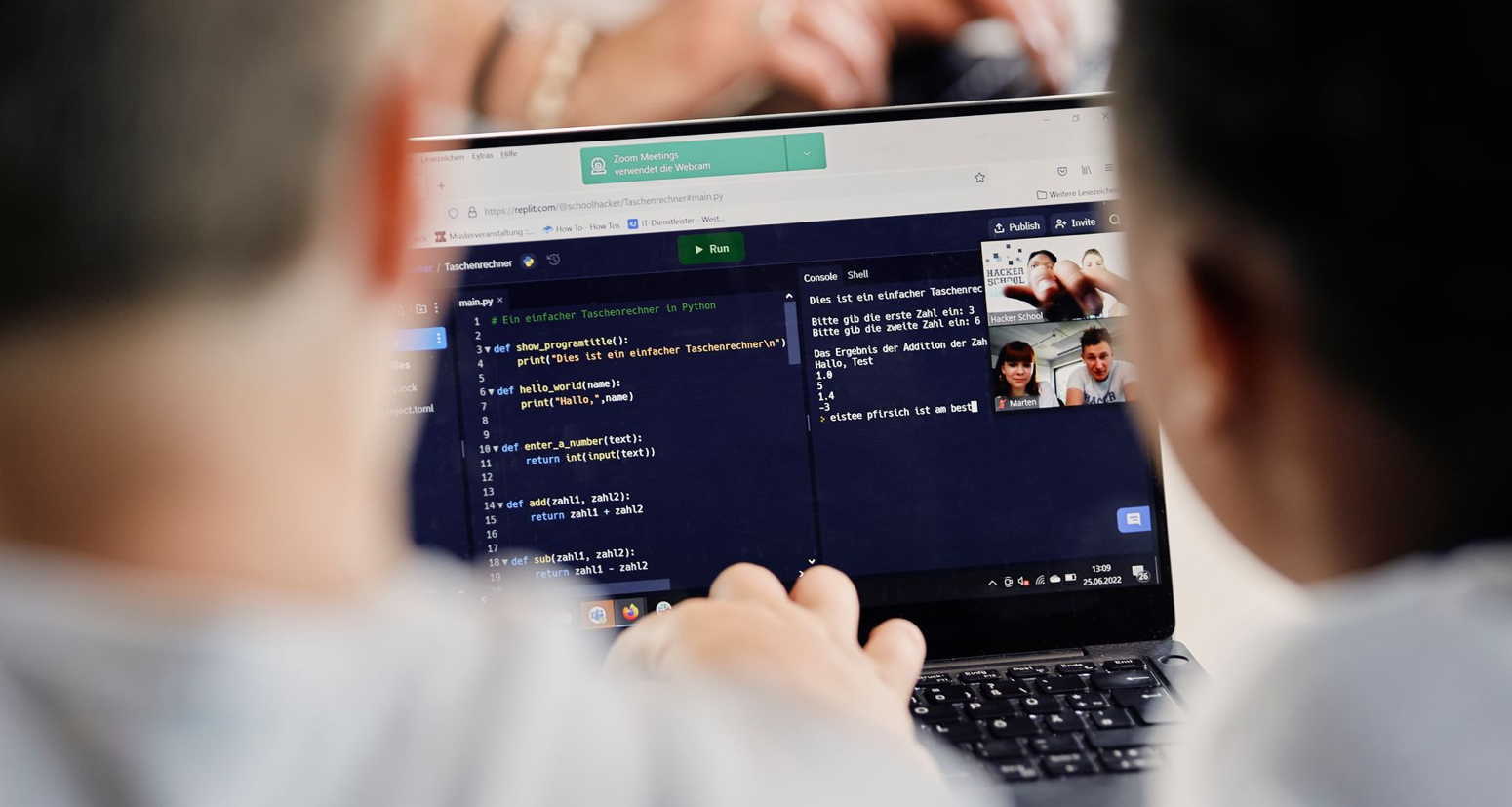
Digitale Grundkenntnisse und Basisfähigkeiten im Programmieren vermitteln zu können, ist eine der Herausforderungen, vor denen Schulen heutzutage stehen. Um Schülerinnen auf ein Leben in einer stetig digitaler werdenden Gesellschaft und […]

Hallo liebe ZUM.de-Community! Heute hatte ich das Vergnügen, an einem inspirierenden pädagogischen Tag teilzunehmen, bei dem Förderlehrkräfte ihre besten Tipps und Tricks austauschten, wie sie Schülerinnen und Schüler unterstützen können, deren […]

Vom 6.-8.März fand das OERCamp in Hamburg statt. Bereits im Teil 1 haben wir über unsere Eindrücke geschrieben. Patricks Fazit war so lang, dass wir es als eigenen Blogpost veröffentlichen. […]

Vom 6.-8.März fand das OERCamp in Hamburg statt. Trotz widriger Umstände (Bahnstreik) waren wir mit großem Team vor Ort. Es war eine Freude, so viele bekannte Gesichter wieder zu treffen […]

In diesem Lernpfad bekommst Du einen Einblick in verschiedene Berufe und erkundest, bei welchen Aufgaben in diesen Berufen Mathematik wichtig wird. Der Lernpfad besteht aus vier Kapiteln, die jeweils einen […]

In diesem Lernpfad (oder auch Stationenlernen) kannst Du vieles über das Alte Ägypten lernen. Durch die günstige Lage am Nil entwickelte sich eine Hochkultur mit Schrift, einheitlicher Religion und den […]

Du hast bereits gelernt, was Funktionen sind und dabei besonders die Linearen Funktionen unter die Lupe genommen. In diesem Lernpfad geht es darum, Eigenschaften einer weiteren Art von Funktionen zu […]
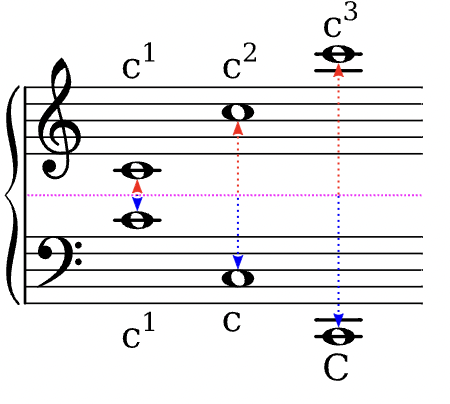
Auf dieser Seite entsteht eine Sammlung von musikalischen Fachbegriffen, wie sie im Kernlehrplan des Landes NRW gebraucht werden. Die Eintragungen erfolgen sukzessiv …


